If lines belong to several fare systems, many possibilities will potentially occur for the selection of fare systems (and therefore tickets) on a connection. The following examples show typical situations, where such multiple-allocation is necessary.
To systematically compare and determine all possibilities, fare systems also receive ranks, which expresses a specified order. First however, an example which does not need any ranks:
Example: Fare calculation for ambiguous fare systems, trip to C Town, part 1
Let's consider the following path legs:
|
From |
To |
Line (TSys) |
Fare system |
|
A Town bus terminal |
A Town main station |
Bus 42 (Bus) |
City |
|
A Town main station |
B Town |
Regional train |
City or Rail |
|
B Town |
C Town |
Intercity |
Rail |
It is assumed, that on the middle path leg both City and Rail ticket types can be used, in particular all stops up to and including B Town belong to fare zones of the fare system City.
The total path can therefore be used in two different ways (fare systems City-City-Rail or fare systems City-Rail-Rail), and the passenger selects the inexpensive one of the two.
Note: In each of the two variants the regional train ticket may also apply for the path leg directly before or after the used line – exactly then when the "fare-reference" of your fare system (City or Rail) is "Each group of contiguous path legs" or even "All path legs together". This aspect is however, not subject of the example
If no ranks are assigned to the fare systems, all fare systems have the default rank 1, and there is no hierarchical order. All possibilities have to therefore be examined and the most inexpensive used, which is what this example wants.
Example: Fare calculation for ambiguous fare systems, trip only to B Town
Let's now look at the case, that the trip already ends in B Town:
|
From |
To |
Line (TSys) |
Fare system (with rank) |
|
A Town bus terminal |
A Town main station |
Bus 42 (Bus) |
City (#1) |
|
A Town main station |
B Town |
Regional train |
City (#1) or Rail (#2) |
The validity range of the fare system City is not left and we assume, that the regional train in this case, is only allowed to be used with tickets from this fare system. This even applies if it were more inexpensive to buy a Rail ticket from the main station.
To model this ranking in Visum, the fare system City must have a higher rank (for example 1), than the fare system Rail (for example 2). Within the fare calculation the fare systems are regarded in descending rank order and the highest ranking used, which is applicable. Because for the rank 1 fare system a valid ticket already exists in this example, the rank 2 variant is not even reviewed.
Example: Fare calculation for ambiguous fare systems, trip to C Town, part 2
What does this definition of ranks now imply for the previous example, where explicitly both fare systems could be applied for the regional train line?
|
From |
To |
Line (TSys) |
Fare system (with rank) |
|
A Town bus terminal |
A Town main station |
Bus 42 (Bus) |
City (#1) |
|
A Town main station |
B Town |
Regional train |
City (#1) or Rail (#2) |
|
B Town |
C Town |
Intercity |
Rail (#2) |
Compared to the case, that the trip ends in B Town, it is not possible to use the entire connection within the prior-ranking fare system City, because the intercity to C Town is not included. A rank 2 fare system is therefore inevitable on this path. This is the starting point for a definition of ranks of fare system combinations, which enable maximum flexibility when modeling such fare conditions.
|
Note: The rank of a combination of fare systems T = {t1, t2,…, tn} is defined as the maximum rank of one of its fare systems: Rank(T) := maxiRank(ti). With this specification one obtains an order on the set of all fare system combinations. This means in the course of fare calculation, Visum regards all of them and selects the most inexpensive total fare. Only if there are no valid combinations for a rank, will the combinations of the next lowest rank be considered. The global fall-back fare is only applied if no valid combination exists. This can be assigned with a value such as -1, to easily identify paths without valid ticket(s) after an assignment. If fares incur an assignment in the impedance definition, please note that a higher fall-back fare (e.g. 99999) prevents paths without a valid ticket(s) from being found and loaded. |
In the example, fare system combinations City-City-Rail and City-Rail-Rail are possible. Their ranks are the same, because max {1, 1, 2} = 2 and max {1, 2, 2} = 2. That is why none of the two are prior-ranking; the passenger in the regional train is therefore not fixed to the fare system City.
By allocating rank 1 for fare system City and rank 2 for fare system Rail, it was overall achieved that the regional train within the City network can only be used with City tickets, but for trips across the network boundaries, it can also be used within the Rail fare system.
Example: Fare calculation for ambiguous fare systems, trip from C Town to A Town bus terminal, part 3
As in the previous example, for the trip in the opposite direction the same combinations of the same rank are returned from which the fare with the most favorable total fare is chosen. It is assumed, that a combination costs 35 € (Rail) plus 5 € (City-City), i.e. 40 €, whereas the other variant costs 40 € (Rail-Rail) plus 2 € (City), i.e. 42 €. On the basis of the previous assumptions it follows, that the fare for Rail-City-City is chosen. This choice presumes the pedestrians' full knowledge of all available fares. In reality, however, this is not always the case. Particularly it can be assumed, that visitors and other groups do not have detailed knowledge of regional fares like the City fare in our example, whereas the supra-regional Rail fare is well-known. To model, for example, that a passenger uses a certain fare system (which is Rail in the example) for a trip section which is as long as possible, the fare is weighted for the selection on the fare system level. This weight helps to determine a "perceived" fare, which is the basis for the selected fare. In other words, fare weights of 1 for the fare system Rail and 10 for City will change the choice, thus the fare Rail-Rail-City will be favorable (perceived fare is 40+20=60 € compared to 85 € for Rail-City-City).
Example: Fare calculation for ambiguous fare systems, trip to C Town, part 4
Let's now look at the variant, that the regional train itself goes to C Town:
|
From |
To |
Line (TSys) |
Fare system (with rank) |
|
A Town bus terminal |
A Town main station |
Bus 42 (Bus) |
City (#1) |
|
A Town main station |
C Town |
Regional train |
City (#1) or Rail (#2) |
In this case it looks as if – exactly like for trips to B Town – the exclusive use of the City fare system is forced. However, this only applies if the City ticket can be bought up to C Town if therefore all stops including C Town lie within fare zones which belong to the zone-based fare of the City fare system. If this is not the case, the attempt to use the connection with fare systems of rank 1 fails, and fare system Rail is applied on the second path leg.
This makes it clear, that the affiliation of a line not automatically indicates, whether it can be used on its entire itinerary with tickets of this fare system. An even clearer example is the following:
Example: Fare network with train fare system in the background
1. Description of the network and the fare conditions:
A regional train line traverses the range of four fare systems (networks), which all together are zone-based fare systems. There are spatial overlaps between the first and the second as well as the second and the third.
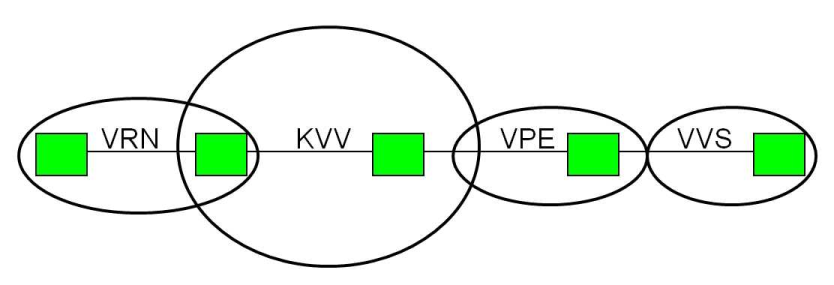
For trips on the regional train line within a fare system, ticket types of this fare system are mandatory. This also applies if parts of the fare system area are traversed, which cover a different fare system. For trips across the boundaries of a fare system, however, ticket types of the fare system Rail long-distance must always be used.
This regulation still leaves the open question, which ticket type to buy if one entirely travels in the covered section of two fare systems. The following regulation applies in this situation: In the covered sections of fare system 2 with fare system 1 and with fare system 3, the latter has precedence.
2. Resulting modeling of the ticket type in Visum:
Because the line can at least be partially used in all five fare systems, it has to be allocated to all fare systems. To express the precedence of fare systems 1 and 3 against fare system 2 in the covered sections of the fare zones, both must have a higher rank (for example 1), than fare system 2 (for example 2). The rank of fare system 4 is not important, it can be set to 3. The non zone-based fare system 5 (Rail long-distance) must have the lowest rank (for example 5), because each of the four zone fare systems have precedence if a trip takes place within it. These ranks have a desired effect on the selection of the ticket type(s) through the following model:
Each zone-based fare system has a specific fare zone type, for example 1, 2, 3 and 4, and corresponding ticket types with fare structure zone-based fare. The spatial overlap of zone fare systems arises in the overlap of their fare zones. All stops served by the line, thus lie exactly in one fare zone or in two fare zones of different types.
This is how you achieve that each of the zone-based ticket types can only be used if all traversed stops lie within fare zones that belong to the fare system of the ticket. Two ticket types can only be used in the covered range of the fare systems and there the fare system ranks provide specified preference. The fare system "Rail long-distance" is used as a fall-back, because a valid ticket can be bought for this one in any case.

